TPU 流变性能测试及胶片挤出过程模拟仿真

        摘要: 利用高压毛细管流变仪对热塑性聚氨酯弹性体( TPU) 熔体的流变性能进行测试分析，建立相应的熔体本构方程。利用polyflow 软件对TPU 熔体在经过优化的衣架型口模内的流动情况进行模拟分析，以检验所用口模的性能，同时采用广义Navier 滑移模型分析不同滑移系数对流动状态的影响。结果表明，Bird-Carreau 模型可以准确描述TPU 熔体的流动行为。在不同温度下，TPU 熔体在模拟所用的衣架型口模中均能实现均匀挤出，并且挤出过程接近壁面无滑移情况。
        复合玻璃在汽车、航空、建筑等领域的应用越来越广泛，这种广泛的应用得益于复合玻璃中间胶层的存在，中间胶层可以吸收冲击、黏附玻璃碎片、保证安全性能［1－4］。传统复合玻璃的中间层黏结材料主要采用聚乙烯缩丁醛( PVB) 胶片，但PVB 胶片的耐低温性能较差，在温度低于零度时，PVB 胶片会迅速表现出脆性，导致黏结性能大幅降低，此外，PVB胶片与有机玻璃的黏结性能也较差，不利于实现复合玻璃的轻量化［5－7］。与传统PVB 胶片相比，新型热塑性聚氨酯弹性体( TPU) 胶片具有更好的耐低温性能，可以显著提高复合玻璃的温度适应性，并且TPU胶片与有机玻璃、聚碳酸酯等材料依然保持着良好的粘接性能［8－10］。在TPU 胶片的挤出过程中，胶片厚度的均匀性是一项非常重要的质量指标，厚度均匀性较差的胶片会降低复合玻璃层间的黏结力，从而大大降低复合玻璃的抗冲击性能。胶片厚度的均匀性与熔体沿模头宽度方向出口流率的均匀性直接相关，及取决于口模流道的设计。因此，通过对TPU 熔体在模头中的流动过程进行模拟仿真，分析模头内的压力场与出口流率分布，可以验证口模流道设计的合理性，并预测挤出胶片厚度均匀性［11－14］。在模拟研究中，TPU 熔体本构方程会对模拟结果的准确性产生较大影响，因此在模拟之前需要得到准确描述TPU 熔体流动状态的本构方程［15］。壁面滑移，是指固体壁面与壁面上黏附的聚合物熔体之间存在着相对切向速度的现象［16］。在传统的挤出成型过程中，通常假设壁面附近的熔体黏附在模具壁面上，即两者之间不存在相对速度。但是从力学角度分析，材料承受的剪切应力不可能无限增大，即存在临界剪切应力，当材料所承受到的力超过临界值时，便会产生壁面滑移现象，完全的壁面不滑移情况并不存在，因此有必要对壁面不滑移假设进行验证［17－18］。
        本文首先利用高压毛细管流变仪得到TPU 熔体的流动数据，通过对流动数据拟合得到TPU 熔体的本构方程。随后，针对经过优化设计的衣架型口模，利用polyflow 软件模拟分析TPU 熔体在该口模内的压力场及沿模头宽度方向的速度场，探究该口模对TPU胶片挤出的适应性，检验其挤出均匀性。同时通过在模拟过程中引入广义Navier 滑移模型，并将模拟得到的结果与实际挤出情况进行对比，探究壁面不滑移假设的合理性。
1 TPU 流变性能及本构方程
        本实验以美国路特润公司生产的TPU 为原料，利用意大利CEAST 公司生产的高压毛细管流变仪对TPU 熔体在170、180、190 ℃三个温度下进行剪切流变测试，得到剪切黏度随剪切速率的变化曲线如图1所示。

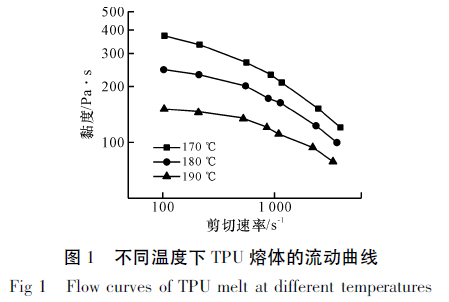
从图中点的分布趋势可以看出，在低剪切速率段，出现第一牛顿平台区，随着剪切速率的提高，TPU 熔体表现出明显的剪切变稀行为，这说明TPU熔体是一种典型的假塑性流体，非牛顿指数小于1，当剪切速率提高时，由于TPU 分子链的解缠与取向作用，导致熔体黏度下降。通过对比不同温度下TPU熔体流动曲线可以看出，随着温度的升高，TPU 熔体黏度下降，黏度随剪切速率的下降趋势也随着温度的升高而变缓。
        为了准确描述第一牛顿平台区与剪切变稀区域内TPU 熔体的流动行为，我们采用Bird-Carreau 模型作为TPU 熔体的本构方程。
        BC 模型表达式为:

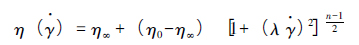
式中，η0－零剪切黏度; η∞ －剪切速率趋近无穷时的剪切黏度; λ－松弛时间; n－非牛顿指数。

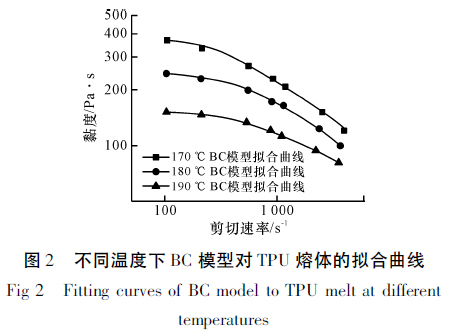
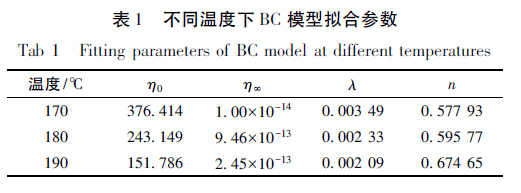
        不同温度下TPU 熔体流动行为的BC 模型拟合曲线如图2 所示。从图中可以看出，BC 模型拟合曲线与TPU 熔体流动行为具有较好的吻合度，说明利用BC 模型可以准确描述TPU 熔体的流动行为。不同温度下BC 模型的拟合参数见表1。从表1 可以看出，随着温度的升高，模型中的零切黏度不断减小，无穷剪切黏度均近似为零，非牛顿系数不断变大，与1 越来越接近，这说明随着温度的升高，TPU 熔体的非牛顿性减弱。

2 流道模型及网格划分

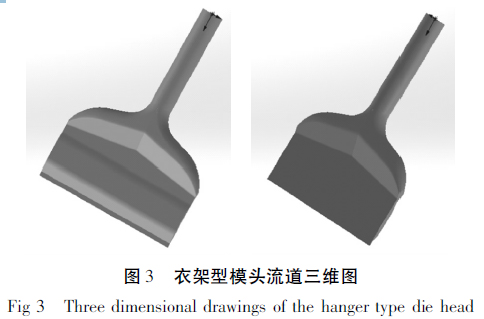
        为了检验所设计的衣架型口模对TPU 片材挤出的适应性，需要在模拟过程中，研究TPU 熔体在该口模中的流动状态。该口模为幅宽200 mm 的衣架型口模，流道三维模型如图3 所示，其中扇形区厚度3mm，松弛区厚度7 mm，模唇区狭缝厚度1. 3 mm，沿流动方向长度300 mm。
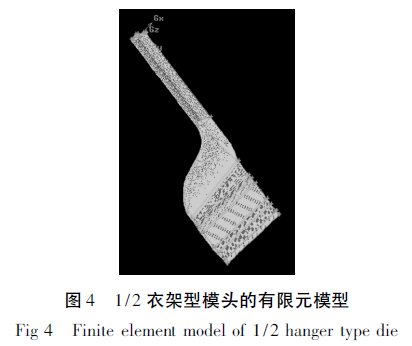
由于流道的对称性，计算时采用1 /2 模型，采用前处理GAMBIT 软件，将流道划分为六面体与四面体混合网格，网格主体为六面体网格，部分过渡区域采用四面体网格。由于与壁面接触的流体流动状态变化较为剧烈，对该处熔体采用边界层进行网格加密。有限元网格模型如图4 所示，整个模型分为124 174 个网格单元。

3 流动过程假设及边界条件
        对TPU 熔体在衣架型口模内的流动做出以下假设: ( 1) 熔体在壁面处无滑移; ( 2) 熔体为不可压缩的非牛顿型流体，密度不变; ( 3) 恒温流动; ( 4)不考虑惯性力和重力; ( 5) 稳态层流。
边界条件设置如下———入口边界条件: inflow;出口边界条件: outflow; 对称面: plane of symmetry;口模壁面: Vn = Vs = 0 ( 在后续考虑壁面滑移问题时设置为Slip conditions) 。
4 结果与讨论
4. 1 不同温度下模拟结果分析
        首先，在假设壁面不滑移的边界条件下，分析挤出流量为3 000 mm3 /s ( 实际流量的一半) 时，熔体温度变化对流道内熔体压力场与速度场的影响，设置170、180、190 ℃三个温度。图5 为模拟计算得到的流道内熔体压力分布云图，不同温度下口模中的压力特征见表2。

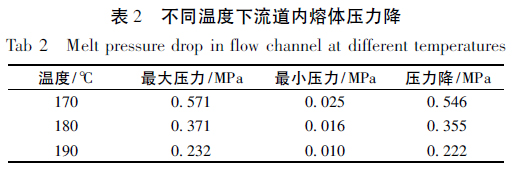
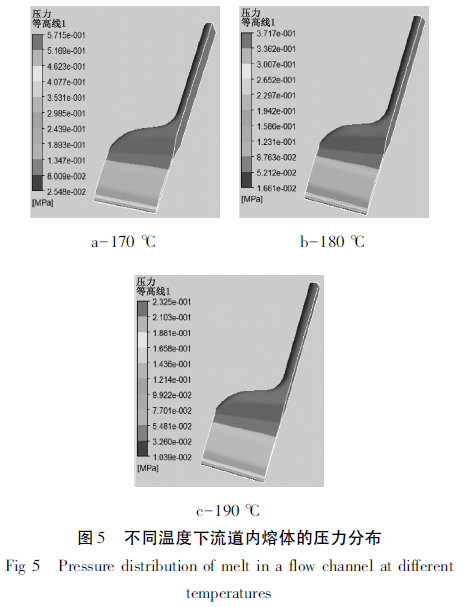
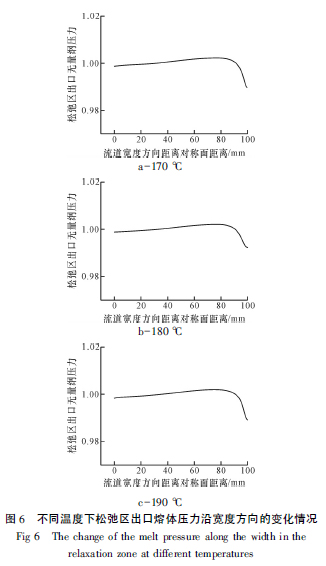
        从图中可以看出，温度为170、180、190 ℃时，压力分布规律相似，沿流动方向存在明显的压力降，而在与流动垂直的方向上，压力变化并不明显。不同温度下的压力降分别为0. 546、0. 355 和0. 222 MPa，即随着温度的升高，整个流道内的压力损失也逐渐减小，而且下降明显。为了更清楚地看出不同温度时整个流道内的压力分布情况，图6 对比了不同温度下松弛区出口处熔体压力沿宽度方向的变化情况。从图中可以看出，沿宽度方向，存在一定的压力梯度，靠近壁面处压力出现一定程度的下降。但从总体上看，这种变化非常微小，波动幅度在2%以内，因此可以认为沿宽度方向压力均匀分布。
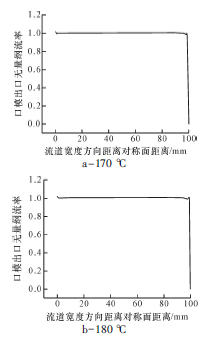
        对于TPU 片材来说，沿模头宽度方向上厚度的均匀性是一项重要的质量指标，而这又直接受熔体在模头宽度方向上速度均匀性的影响。对于这种速度均匀性，我们选取了模头出口宽度方向中线上的无量纲速度分布来表示，结果如图7 所示。从图7 可以看出，不同温度下，出口速度均匀性较好，且较为一致。这也与松弛区出口宽度方向上压力分布的均匀性相对应。因此，该衣架型口模能够均匀挤出TPU片材。

4. 2 壁面滑移对流道内熔体流动行为的影响
        为了验证壁面不滑移假设的合理性，本文以180℃、3 000 mm3 /s 条件下的挤出情况为研究对象，采用广义Navier 滑移模型研究滑移系数对模头内压力场和速度场的影响。Navier 表达式为: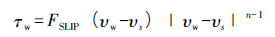式中，υw－壁面的速度; τw－聚合物熔体在壁面的切向剪切应力; υs－聚合物熔体在壁面处的切向速度; n－非牛顿指数; FSLIP －滑移系数。当FSLIP取无穷大时，表示无滑移现象产生，取值越小表示滑移现象越严重。
        模拟过程中，设置一系列滑移系数，分别为500、1 000、3 000、10 000、20 000、30 000。计算得到的不同滑移系数下TPU 熔体在流道内的压力分布情况如图8 所示。

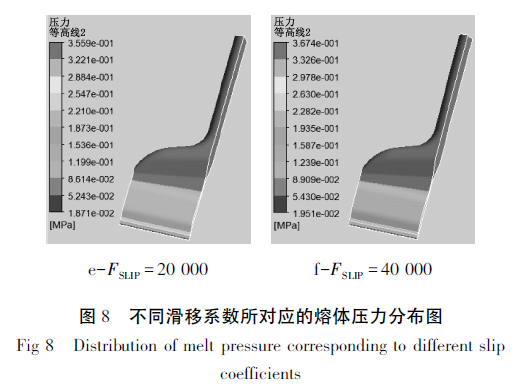
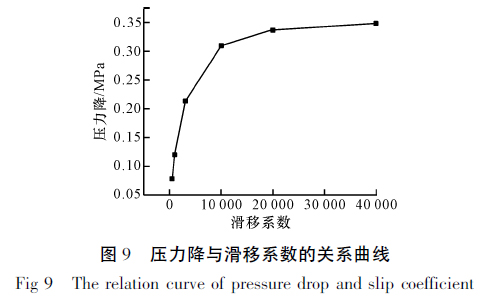
        从图8 可以看出，不同滑移系数下，压力分布规律相似，沿模头宽度方向上压力的变化同样不明显。从图9 可以看出，当滑移系数小于10 000 时，随着滑移系数的增加，熔体压力降也明显增加。但当滑移系数大于10 000 后，滑移系数增加，压力降只发生微小变化，并且当滑移系数FSLIP = 40 000 时，压力降已经达到0. 348 MPa，在实际挤出实验中，测得模头内的压力降约为0. 346 MPa，这说明模头内的滑移情况与滑移系数为40 000 时相接近。在之前的模拟计算中得到，同样温度与挤出流量下，设置不滑移边界条件时，整个模头的压力降为0. 355 MPa，这也与实际压力降近似相同。因此，可以认为在TPU 胶片的挤出过程中，口模内部壁面处不存在壁面滑移现象，之前模拟过程中壁面不滑移的假设具有合理性。

5 结论
        通过对高压毛细管流变仪测得的流变数据进行分析与拟合，可以确定采用Bird-Carreau 模型能够准确地描述所用TPU 熔体的流动行为。利用polyflow 软件对衣架型片材机头内熔体的压力场和速度场进行模拟分析结果表明，经过优化设计的机头用于挤出TPU片材时，出口速度的横向分布基本均匀，机头内部几乎不存在壁面滑移现象，在模拟分析时壁面不滑移的假设具有合理性。